സ്ഫുടം
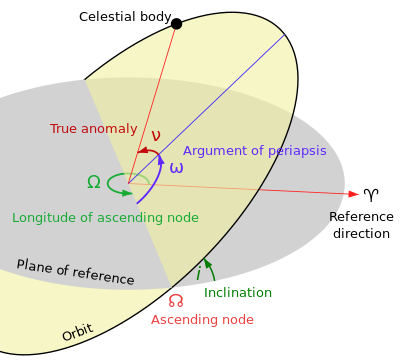
ഏതെങ്കിലും ഒരു നിശ്ചിതസമയത്തു് ഒരു ഖഗോളവസ്തുവിനു് അതിന്റെ ഭ്രമണപഥത്തിൽ ഒരു മൂലബിന്ദു(origin)വിൽനിന്നുമുള്ള ആപേക്ഷികകോണീയ അകലത്തിനെയാണു് അതിന്റെ സ്ഫുടം(Longitude of the ascending node) എന്നു പറയുന്നതു്. പാശ്ചാത്യരീതിയനുസരിച്ച് സ്ഫുടത്തിനു് ആധാരമായ മൂലബിന്ദു ക്രാന്തിവൃത്തത്തിലെ മേഷാദി(First point of Aries) ആണു്. ഇങ്ങനെ ലഭിക്കുന്ന അളവിനു് സായനസ്ഫുടം എന്നു പറയുന്നു. എന്നാൽ ഭാരതീയരീതികളിൽ, ഈ മൂല്യത്തിനൊപ്പം അയനാംശം കൂടി പരിഗണിച്ച ഫലമാണു് കണക്കിലെടുക്കുന്നതു്. ഇതിനെ നിരയനസ്ഫുടം എന്നുപറയുന്നു.
സ്ഫുടത്തിന്റെ ഉപയോഗം
തിരുത്തുക- . ബഹിരാകാശഗവേഷണത്തിൽ വിവിധ ഖഗോളവസ്തുക്കളുടെ സ്ഥാനം, പ്രവേഗം, അകലം, അവയുടെ ഭ്രമണപഥത്തിന്റെ ആകൃതിയും സ്ഥാനവും, അവയുടെ ഗതിയിൽ ഉണ്ടാകാവുന്ന വ്യത്യാസം തുടങ്ങിയവ അറിയാൻ.
- . വാനനിരീക്ഷകർക്കു് വിവിധ ഖഗോളവസ്തുക്കളുടെ സ്ഥാനം മുൻകൂട്ടി അറിഞ്ഞ്, ദൂരദർശിനി തുടങ്ങിയ അവരുടെ ഉപകരണങ്ങൾ ക്രമീകരിക്കാൻ.
- . പഞ്ചാംഗം, കലണ്ടർ തുടങ്ങിയവ തയ്യാറാക്കുമ്പോൾ വർഷം, മാസം, ദിവസം തുടങ്ങിയവയുടെ കൃത്യമായ പ്രാരംഭവും ഗ്രഹയോഗങ്ങളും മറ്റും അറിയാൻ.
മേഷാദി
തിരുത്തുകഭൂമിയുടെ അച്ചുതണ്ടിനു ലംബമായും ഭൂമദ്ധ്യരേഖയ്ക്കു സമകേന്ദ്രീയമായും (concentric) ആകാശത്തിലൂടെ കടന്നുപോകുന്നതായി സങ്കൽപ്പിക്കാവുന്ന ഒരു മഹാവൃത്തമാണു് ഖഗോളമദ്ധ്യരേഖ (celestial equator). ഭൂമദ്ധ്യരേഖയിൽ നിൽക്കുന്ന ഒരാളെസംബന്ധിച്ചിടത്തോളം ഈ രേഖ കടന്നുപോകുന്നതു് ചക്രവാളത്തിലെ പടിഞ്ഞാറേ അറ്റത്തുനിന്നും അയാളുടെ ഉച്ചിയിലൂടെ (തലയ്ക്കുമുകളിലുള്ള ദിശയിൽ ആകാശത്തിന്റെ പരകോടി - zenith) ചക്രവാളത്തിന്റെ കിഴക്കേ അറ്റം വഴി ഭൂമിയുടെ എതിർവശത്തു് (കാൽച്ചുവടിന്റെ ദിശയിൽ) അധോലംബബിന്ദു(nadir)വഴി തിരിച്ച് പടിഞ്ഞാറെ ചക്രവാളബിന്ദുവിൽ എത്തുന്ന സാങ്കൽപ്പികരേഖയാണു് ഈ മഹാവൃത്തം.
എന്നാൽ ഈ ഖഗോളമദ്ധ്യരേഖയുടെ അതേ തലത്തിലല്ല ഭൂമി സൂര്യനെ പ്രദക്ഷിണം വെക്കുന്ന ഭ്രമണപഥം. ഏകദേശം 23.5 ഡിഗ്രി ചെരിവ് (obliquity of the orbit) ഈ രണ്ടു തലങ്ങളുമായുണ്ടു്. അതുകൊണ്ടു് സൂര്യനും സൗരയൂഥത്തിലുള്ള മറ്റംഗങ്ങളും ഭൂമിക്കുചുറ്റും കറങ്ങുന്നതായി തോന്നുന്നതു് മറ്റൊരു വൃത്തത്തിലൂടെയാണു്. ഈ വൃത്തത്തിനെയാണു് ക്രാന്തിവൃത്തം എന്നു പറയുന്നതു്.
ഖഗോളമദ്ധ്യരേഖയും ക്രാന്തിവൃത്തവും തമ്മിൽ പരസ്പരം മുറിച്ചുകടന്നുപോകുന്നതിനാൽ പരസ്പരം എതിർദിശയിൽ നിൽക്കുന്ന രണ്ടു ബിന്ദുക്കളിൽ ഇവ സംഗമിക്കേണ്ടതാണു്. ഈ ബിന്ദുക്കളെ വിഷുവങ്ങൾ (points of equinox) എന്നു വിളിക്കാം.
ഇതിൽ ഒരു ബിന്ദുവാണു് മേഷാദി അഥവാ മഹാവിഷുവം (first point of Aries). ജ്യോതിഃശാസ്ത്രത്തിലും ജ്യോതിഷത്തിലും ഖഗോളഗണിതത്തിൽ ഏറ്റവും പ്രാഥമികമായ മൂലബിന്ദുവായി മേഷാദിയെ പരിഗണിക്കുന്നു. മേഷാദിയിൽനിന്നും ഒരു ഖഗോളവസ്തുവിലേക്കുള്ള സ്ഥാനവ്യത്യാസമാണു് ആ ഖഗോളവസ്തുവിന്റെ രേഖാംശം നിർണ്ണയിക്കുന്നതു്. ഈ രേഖാംശം തന്നെയാണു് സ്ഫുടം എന്നും അറിയപ്പെടുന്നതു്.
സ്ഫുടത്തിന്റെ ചരസ്വഭാവം
തിരുത്തുക(ഉദാഹരണങ്ങളിൽ കൊടുത്തിട്ടുള്ള വിലകൾ ഏകദേശം മാത്രമാണു്. ഇവയിൽ ഖഗോളസംബന്ധമായ മറ്റു ഘടകങ്ങളുടെ സ്വാധീനം മൂലം ഏറ്റക്കുറച്ചിലുകളുണ്ടാകാം).
ഖഗോളവസ്തുവിനു് ഒരു പൂർണ്ണപ്രദക്ഷിണം ചെയ്യാൻ ആവശ്യമായ ഇടവേളയ്ക്കും അതിന്റെ ഭ്രമണപഥത്തിന്റെ ആകൃതിയ്ക്കും അനുസരിച്ച് സ്ഫുടം മാറിക്കൊണ്ടിരിക്കും. ഉദാഹരണത്തിനു് ഭൂമിയിൽനിന്നു നോക്കുമ്പോൾ സൂര്യൻഏകദേശം 365.25 കലണ്ടർ ദിവസങ്ങൾകൊണ്ടാണു് ക്രാന്തിവൃത്തം ഒരു തവണ (360 ഭാഗ അഥവാ ഡിഗ്രി) പ്രദക്ഷിണം പൂർത്തിയാക്കുന്നതു്. അതായതു് ഓരോ ദിവസവും സൂര്യന്റെ സ്ഫുടത്തിൽ ഒരു ഡിഗ്രിയിലും സ്വല്പം കൂടുതൽവെച്ച് സ്ഫുട്ംമാറിക്കൊണ്ടിരിക്കുന്നുണ്ടു്. ചന്ദ്രൻ ഏകദേശം 27.32 ദിവസംകൊണ്ടു് ഒരു പ്രദക്ഷിണം പൂർത്തിയാക്കുന്നതിനാൽ അതിന്റെ പ്രതിദിനസ്ഫുടം ശരാശരി 360/27.32 = 13.18 ഡിഗ്രി ആയിരിക്കും. ഇവ തന്നെ വർഷത്തിന്റെ എല്ലാ സമയത്തും ഒരുപോലെയായിരിക്കില്ല.
ഭൂമിയെ സംബന്ധിച്ചിടത്തോളം, സൗരയൂഥത്തിൽനിന്നും വളരെവളരെയകലെ സ്ഥിതിചെയ്യുന്ന നക്ഷത്രങ്ങളുടേയും മറ്റും ആപേക്ഷികസ്ഥാനചലനം തീരെ നിസ്സാരമാണു്. അതിനാൽ അവയുടെ സ്ഫുടങ്ങൾ പ്രായോഗികമായി സ്ഥിരമായിരിക്കും. (എന്നാൽ ആയിരക്കണക്കിനു കൊല്ലങ്ങളിൽ ഇതും കുറേശ്ശെ വ്യത്യാസപ്പെട്ടുകൊണ്ടിരിക്കും).
സായനസ്ഫുടം
തിരുത്തുകക്രാന്തിവൃത്തത്തിലെ ഒരു നിശ്ചിതബിന്ദു ( മേഷാദി)വിൽ നിന്നും ഒരു നിശ്ചിത സമയത്തുള്ള ഒരു ഖഗോളത്തിന്റെ കോണീയ അകലമാണു് സായനസ്ഫുടം.
ആധുനികകാലത്തു് ഖഗോളഗണിതത്തിൽ വ്യാപകമായും പ്രായോഗികമായും ഉപയോഗിക്കുന്നതു് മേഷാദിയേയോ ക്രാന്തിവൃത്തത്തിലെ മറ്റേതെങ്കിലും സ്ഥിരബിന്ദുവിനെയോ അടിസ്ഥാനമാക്കിയുള്ള നിർദ്ദേശാങ്കങ്ങളാണു്. ലോകത്തിലെ പല രാജ്യങ്ങളും സമൂഹങ്ങളും കാലഗണനത്തിൽ വർഷം, മാസം, നക്ഷത്രം, തിഥി തുടങ്ങിയവയുടെ ആരംഭവും ദൈർഘ്യവും അളക്കാൻ ഈ വ്യവസ്ഥ അനുസരിച്ചുള്ള സായനസ്ഫുടമാണു് സ്വീകരിച്ചിരിക്കുന്നതു്.
അയനാംശം
തിരുത്തുകഎന്നാൽ ചില കലണ്ടറുകളിലും പഞ്ചാംഗങ്ങളിലും അയനാംശം എന്നൊരു ഘടകം കൂടി ഉൾപ്പെടുത്തിയിട്ടുണ്ടു്. മിക്കവാറും ഭാരതീയസമ്പ്രദായങ്ങളും ആര്യഭടൻ, വരാഹമിഹിരൻ, ബ്രഹ്മഗുപ്തൻ തുടങ്ങിയ ഭാരതീയ ജ്യോതിശാസ്ത്രജ്ഞരും സൂര്യസിദ്ധാന്തം തുടങ്ങിയ ഗണിതപദ്ധതികളും വഴി നിർദ്ദേശിക്കപ്പെടുന്ന പഞ്ചാംഗങ്ങളിൽ അയനാംശം കൂടി പരിഗണിക്കപ്പെടുന്നു.
പുരസ്സരണം, അക്ഷഭ്രംശം തുടങ്ങിയ ചാഞ്ചാട്ടങ്ങൾ മൂലം ഭൂമിയുടെ അച്ചുതണ്ടോ അതിനെ അടിസ്ഥാനമാക്കി നിർണ്ണയിച്ചിട്ടുള്ള ധ്രുവങ്ങളോ ഭൂമദ്ധ്യരേഖയോ ഖഗോളമദ്ധ്യരേഖതന്നെയോ കേവലമായി സ്ഥിരമല്ല. ഇവയെല്ലാമടങ്ങുന്ന മൊത്തം ചട്ടക്കൂട് വളരെ സാവധാനത്തിൽ ചാഞ്ചാടിക്കൊണ്ടിരിക്കുന്നു എന്നു പറയാം. ഈ ചാഞ്ചാട്ടം മൂലം ഖഗോളമദ്ധ്യരേഖയ്ക്കു് ക്രാന്തിവൃത്തവുമായുള്ള ചെരിവും തദ്ഫലമായി അവയ്ക്കു പരസ്പരമുള്ള സംഗമബിന്ദുക്കൾ (മേഷാദിയും തുലാവിഷുവവും) തന്നെ സാവധാനത്തിൽ നീങ്ങിക്കൊണ്ടിരിക്കുന്നുണ്ടു്. ഇവയിൽ ഏറ്റവും മുഖ്യമായ സ്വാധീനം, ഏകദേശം 26000 വർഷങ്ങൾകൊണ്ടു് ഒരാവൃത്തി പൂർത്തീകരിക്കുന്ന പുരസ്സരണം (ഖഗോളായനം) (precession)എന്ന പ്രതിഭാസത്തിനാണു്.
പുരസ്സരണത്തിന്റെ പ്രഭാവം മൂലം മേഷാദി എന്ന മൂലബിന്ദുതന്നെ മാറിക്കൊണ്ടിരിക്കുന്നുണ്ടു്. ഈ വ്യത്യാസമാണു് അയനാംശം.
നിരയനസ്ഫുടം
തിരുത്തുകസാധാരണ സ്ഫുടത്തിന്റെ(സായനസ്ഫുടം)കൂടെ അയനാംശം കൂടി പരിഗണിച്ച് സൂക്ഷ്മമായി കണ്ടുപിടിക്കുന്ന ഗണിതസമ്പ്രദായമാണു് നിരയനസ്ഫുടം.
സൗരയൂഥത്തെ (അതിനുള്ളിലെ എല്ലാ അംഗങ്ങളേയും ഒരുമിച്ചു ചേർത്ത്) പരസ്പരാകർഷണം കൊണ്ടു് അന്യോന്യം ബന്ധിക്കപ്പെട്ട ഒരുകൂട്ടം പന്തുകളായി സങ്കൽപ്പിക്കുക. ഈ കൂട്ടത്തെത്തന്നെ മൊത്തം ഒരു പന്തായി വിചാരിക്കാവുന്നതാണു്. അങ്ങനെയുള്ള ഒരു പന്തു് മൊത്തം പ്രപഞ്ചത്തെയോ ആകാശഗംഗയേയോ ഏറ്റവും അടുത്തുള്ള നക്ഷത്രത്തെപ്പോലുമോ സംബന്ധിച്ചിടത്തോളം, അവയിൽനിന്നെല്ലാം സ്വതന്ത്രമായി, സ്വന്തമായ ഒരു ചട്ടക്കൂടിലാണെന്നു പറയാം. പുറത്തുള്ള ഗോളങ്ങളുമായുള്ള ദൂരമോ ഗുരുത്വാകർഷണപ്രഭാവമോ ഈ ചട്ടക്കൂടിന്റെ അകത്തെ വ്യവസ്ഥയെ ബാധിക്കാത്തത്ര നിസ്സാരമാണു്. അതായതു് ചട്ടക്കൂടിന്റെ അകത്തെ അംഗങ്ങൾ തമ്മിലുള്ള പരസ്പരാകർഷണങ്ങളെയോ പ്രവേഗങ്ങളെയോ ചലനാവൃത്തികളേയോ നക്ഷത്രാന്തരബാഹ്യലോകം മിക്കവാറും ഒട്ടുംതന്നെ സ്വാധീനിക്കുന്നില്ല. അതിനാൽ ക്രാന്തിവൃത്തത്തിനു പുറത്തുള്ള ഒരു നിർദ്ദേശാങ്കവ്യവസ്ഥയ്ക്കോ മൂലബിന്ദുവിനോ മനുഷ്യരുടെ പ്രായോഗികശാസ്ത്രത്തിലും ഗവേഷണപര്യവേക്ഷണങ്ങളിലും ഒട്ടും പ്രസക്തിയില്ല എന്നു പറയാം.
ഇക്കാരണംകൊണ്ടു് ബഹിരാകാശഗവേഷണം, ബഹിരാകാശപര്യവേക്ഷണം, വാനനിരീക്ഷണം, കാലാവസ്ഥ തുടങ്ങിയ മേഖലകളിൽ നിരയനസ്ഫുടം പരിഗണിക്കാറില്ല. എന്നാൽ പ്രപഞ്ചസ്ഥിരസമയം, നക്ഷത്രാന്തരസമയം എന്നിവ കണക്കുകൂട്ടുമ്പോൾ ഗവേഷണസ്ഥാപനങ്ങളും മറ്റും തത്തുല്യവും അനുയോജ്യവുമായ തിരുത്തലുകൾ (clock corrections) നടത്താറുണ്ടു്.
തങ്ങളുടെ സമൂഹത്തിൽ പ്രചാരത്തിലുള്ള പഞ്ചാംഗങ്ങളുടെ കാലഗണനയും ഫലജ്യോതിഷവും ലക്ഷ്യമാക്കി സ്ഫുടം കണക്കാക്കുമ്പോൾ ഭാരതത്തിൽ അടക്കം പല പഞ്ചാംഗവ്യവസ്ഥകളിലും നിരയനസ്ഫുടരീതി അവലംബിക്കുന്നുണ്ടു്.
