സമഎൻട്രോപിക പ്രക്രിയ
ഈ ലേഖനം ലുവ പിഴവ് package.lua-ൽ 80 വരിയിൽ : module 'Module:ISO 639 name/ISO 639-5' not found ഭാഷയിൽ നിന്ന് കൃത്യമല്ലാത്ത/യാന്ത്രികമായ പരിഭാഷപ്പെടുത്തലാണ്. ഇത് ഒരു കമ്പ്യൂട്ടറോ അല്ലെങ്കിൽ രണ്ട് ഭാഷയിലും പ്രാവീണ്യം കുറഞ്ഞ ഒരു വിവർത്തകനോ സൃഷ്ടിച്ചതാകാം. |
എൻട്രോപി അഥവാ ഉത്ക്രമം മാറ്റമില്ലാതെ തുടരുന്ന പ്രക്രിയകളെയാണ് താപഗതികത്തിൽ സമഎൻട്രോപിക പ്രക്രിയ (Isentropic process) അഥവാ സമഉത്ക്രമപ്രക്രിയ എന്നുപറയുന്നത്. ഇത് ഒരു താപബദ്ധപ്രക്രിയയാണെന്നുമാത്രമല്ല ഈ പ്രക്രിയ പ്രത്യാവർത്തനീയവുമാണ്(Reversible). താപനഷ്ടമോ ഘർഷണം മൂലമുളള നഷ്ടമോ പൂർണമായും ഇല്ലാതാക്കിക്കൊണ്ട് പ്രായോഗികതലത്തിൽ യാതൊരു പ്രക്രിയകളും തന്നെ സാധ്യമല്ലാത്തതിനാൽ ഇത് ഒരു ആദർശപ്രക്രിയമാത്രമാണ്.[1][2][3][4][5][6] ഇതിൽ, വ്യൂഹത്തിന്റെ പ്രവൃത്തികൈമാറ്റങ്ങളെല്ലാം തന്നെ ഘർഷണരഹിതമാണെന്നും, താപമോ ദ്രവ്യമോ കൈമാറ്റം ചെയ്യപ്പെടുന്നുല്ലെന്നുമാണ് അനുമാനിക്കപ്പെടുന്നത്. യഥാർത്ഥ പ്രക്രിയകളെ താരതമ്യം ചെയ്യുന്നതിനുളള മോഡലുകളായി ഇത്തരം ആദർശപ്രക്രിയകളെ ഉപയോഗപ്പെടുത്താവുന്നതാണ്.[7]
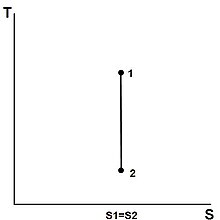
ഒരു പ്രക്രിയ പ്രത്യാവർത്തനീയവും താപബദ്ധവുമാണെങ്കിൽ അതിലെ പിണ്ഡത്തിന്റെ എൻട്രോപ്പിക്ക് മാറ്റം വരുകയില്ല. എൻട്രോപ്പി മാറ്റമില്ലാതെ നിലനില്ക്കുന്ന ഇത്തരം പ്രക്രിയകളെല്ലാം സമഎൻട്രോപിക പ്രക്രീയകളാണ്.
ഗണിതപരമായി, ഇതിനെ അല്ലെങ്കിൽ എന്നിങ്ങനെ സൂചിപ്പിക്കുന്നു.[8] പമ്പുകൾ, വാതകകമ്പ്രസ്സറുകൾ, ടർബൈനുകൾ, നോസിലുകൾ, ഡിഫ്യൂസറുകൾ എന്നിവ സമഎൻട്രോപിക ഉപകരണങ്ങളാണ്.
സ്ഥിതപ്രവാഹ ഉപകരണങ്ങളുടെ സമോത്ക്രമ ദക്ഷത
തിരുത്തുകമിക്ക സ്ഥിതപ്രവാഹ (steady flow) ഉപകരണങ്ങളും താപബദ്ധ അവസ്ഥകളിലാണ് പ്രവർത്തിക്കുന്നത്, കൂടാതെ ഈ ഉപകരണങ്ങളുടെ ആദർശപ്രക്രിയ സമോത്ക്രമപ്രക്രിയയാണ്. ഒരു ഉപകരണത്തിന് സമോത്ക്രമ ഉപകരണത്തിന്റെ ദക്ഷതയോട് എത്രത്തോളം താദാത്മ്യം ഉണ്ട് എന്ന് വ്യാഖ്യാനിക്കുന്ന പ്രാചര(parameter)മാണ് അതിന്റെ സമോത്ക്രമ ദക്ഷത അഥവാ താപബദ്ധ ദക്ഷത.[9]
ടർബൈനിൻ്റെ സമോത്ക്രമ ദക്ഷത (Isentropic efficiency):
കംപ്രസറുകളുടെ സമോത്ക്രമ ദക്ഷത:
നോസിലുകളുടെ സമോത്ക്രമ ദക്ഷത:
മുകളിത്തെ എല്ലാ സമവാക്യങ്ങൾക്കും:
- പ്രവേശഘട്ടത്തിലെ വിശിഷ്ട എന്താൽപി,
- യഥാർത്ഥ പ്രക്രിയുടെ നിർഗ്ഗമനഘട്ടത്തിലെ വിശിഷ്ട എന്താൽപി,
- സമോത്ക്രമപ്രക്രിയയുടെ നിർഗ്ഗമനഘട്ടത്തിലെ വിശിഷ്ട എന്താൽപി.
താപഗതിക പരിചക്രങ്ങളിലെ സമോത്ക്രമ ഉപകരണങ്ങൾ
തിരുത്തുക| Cycle | Isentropic step | Description |
|---|---|---|
| ആദർശ റാൻകൈൻ പരിചക്രം | 1→2 | ഒരു പമ്പിനുളളിലെ സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ റാൻകൈൻ പരിചക്രം | 3→4 | ഒരു ടർബൈനിനുളളിലെ സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ കാർനോട്ട് പരിചക്രം | 2→3 | സമോത്ക്രമ വികാസം |
| ആദർശ കാർനോട്ട് പരിചക്രം | 4→1 | സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ ഓട്ടോ പരിചക്രം | 1→2 | സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ ഓട്ടോ പരിചക്രം | 3→4 | സമോത്ക്രമ വികാസം |
| ആദർശ ഡീസൽ പരിചക്രം | 1→2 | സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ ഡീസൽ പരിചക്രം | 3→4 | സമോത്ക്രമ വികാസം |
| ആദർശ ബ്രേയ്ട്ടൻ പരിചക്രം | 1→2 | ഒരു വാതകകമ്പ്രസ്സറിനുളളിലെ സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ ബ്രേയ്ട്ടൻ പരിചക്രം | 3→4 | ഒരു ടർബൈനിനുളളിലസമോത്ക്രമ വികാസം |
| ആദർശ ബാഷ്പ സമ്മർദ്ദ റെഫിജറേഷൻ പരിചക്രം | 1→2 | ഒരു വാതകകമ്പ്രസ്സറിനുളളിലെ സമോത്ക്രമ സമ്മർദ്ദനം |
| ആദർശ ലീനോയിർ പരിചക്രം | 2→3 | സമോത്ക്രമ വികാസം |
കുറിപ്പ്: ഇത്തരം സമോത്ക്രമ സങ്കല്പനങ്ങൾ ആദർശപരിചക്രങ്ങളിൽ മാത്രമേ പ്രായോഗികമാകുകയുളളു.യഥാർത്ഥവ്യൂഹങ്ങൾ ഒരിക്കലും സമോത്ക്രമമല്ല, എന്നാൽ അവ സമോത്ക്രമമാണെന്ന് സങ്കല്പിക്കുന്നത് വിവിധ കണക്കുകൂട്ടലുകൾക്കുപകരിക്കും.
സമോത്ക്രമപ്രവാഹം
തിരുത്തുകദ്രവങ്ങളുടെ താപബദ്ധവും പ്രത്യാവർത്തനീയവുമായ പ്രവാഹത്തിനെയാണ് സമോത്ക്രമപ്രവാഹം എന്നുപറയുന്നത്. അതായത് ആ പ്രവാഹത്തിലേയ്ക്ക് താപകൈമാറ്റമോ അതുമല്ലെങ്കിൽ ഘർഷണം, അപവ്യയം എന്നിവമൂലമുളള ഊർജ്ജകൈമാറ്റമോ സംഭവിക്കുന്നില്ല. എന്നാൽ താപത്തിന്റെ രൂപത്തിലല്ലാതെ സമോത്ക്രമപ്രക്രിയയിൽ ഊർജ്ജകൈമാറ്റം സാധ്യമാണ്. സമോത്ക്രമസമ്മർദ്ദനമോ വികാസമോ മുഖാന്തിരമുളള പ്രവൃത്തി കൈമാറ്റത്തിലൂടെയാണ് അത് സാധ്യമാകുന്നത്.
സമോത്ക്രമബന്ധങ്ങൾ ഉരുത്തിരിക്കൽ
തിരുത്തുകഒരു സംവൃത വ്യൂഹത്തിന്റെ ആകെ ഊർജ്ജവ്യത്യാസം അത് ചെയ്ത പ്രവൃത്തിയുടെയും അതിലേയ്ക്ക് ചേർക്കപ്പെട്ട താപത്തിന്റെയും തുകയാണ്:
വ്യൂഹത്തിനുണ്ടായ വ്യാപ്തവ്യത്യസം മൂലം അത് ചെയ്ത പ്രതിലോമീയ പ്രവൃത്തിയാണ്:
ഇതിൽ എന്നാൽ മർദ്ദവും, എന്നാൽ വ്യാപ്തവും ആണ്. എന്താൽപിയിലുണ്ടായ മാറ്റം ( ) താഴെപ്പറയും പ്രകാരമാണ്
പ്രതിലോമീയവും താപബദ്ധവുമായ ഒരു പ്രക്രിയിൽ , and so , പ്രതിലോമീയവും താപബദ്ധവുമായ എല്ലാ പ്രക്രിയകളും സമോത്ക്രമപ്രക്രിയകളാണ്. ഇത് രണ്ട് പ്രധാന നിരീക്ഷണങ്ങളിലേയ്ക്ക് നയിക്കുന്നു:
അടുത്തതായി, ആദർശവാതകങ്ങളുടെ സമോത്ക്രമപ്രക്രിയകൾക്ക് ഒരു സുപ്രധാനമായ ബന്ധം കണ്ടെത്താൻ കഴിയും. ആദർശവാതകങ്ങളുടെ ഏതൊരു രൂപാന്തരത്തിനും എല്ലായ്പോഴും,
- , and എന്നായിരിക്കും.
, എന്നിവയ്ക്ക് കണ്ടെത്തിയ മുകളിലെ ഫലങ്ങൾ പ്രകാരം,
അതുകൊണ്ട് ഒരു ആദർശവാതകത്തിന്റെ താപധാരിതാ അംശബന്ധം (heat capacity ratio) ഇങ്ങനെ എഴുതാം,
കലോറികമായി സമ്പൂർണമായ ഒരു വാതകത്തിന് സ്ഥിരാങ്കമായിരിക്കും. കലോറികമായി സമ്പൂർണമായ വാതകമായി അനുമാനിച്ചുകൊണ്ട് മുകളിലത്തെ സമവാക്യത്തെ സമാകലനം ചെയ്താൽ,
അതായത്,
ആദർശവാതകത്തിന്റെ അവസ്ഥാസമവാക്യമായ പ്രകാരം,
(തെളിവ്: എന്നാൽ nR = സ്ഥിരാങ്കം, അതിനാൽ .)
കൂടാതെ , സ്ഥിരമായ (പ്രതി മോളിന്),
- ഉം
അപ്രകാരം ഒരു ആദർശവാതകത്തിന്റെ സമോത്ക്രമപ്രക്രിയയ്ക്ക്,
- അഥവാ
ഒരു ആദർശവാതകത്തിന്റെ സമോത്ക്രമബന്ധങ്ങളുടെ പട്ടിക
തിരുത്തുകതാഴെപ്പറയുന്നവയിൽ നിന്നുമാണ് ഇവ ഉരിത്തിരിക്കപ്പെട്ടത്,
ഇവിടെ:
- = മർദ്ദം,
- = വ്യാപ്തം,
- = വിശിഷ്ടതാപങ്ങളുടെ അംശബന്ധം = ,
- = താപനില,
- = പിണ്ഡം,
- = വാതകസ്ഥിരാങ്കം = ,
- = സാർവത്രികവാതക സ്ഥിരാങ്കം,
- = നിർദ്ദിഷ്ട വാതകത്തിന്റെ തന്മാത്രാപിണ്ഡം,
- = സാന്ദ്രത,
- = സ്ഥിരമർദ്ദത്തിലുളള വിശിഷ്ടതാപം,
- = സ്ഥിരവ്യാപ്തത്തിലുളള വിശിഷ്ടതാപം.
അവലംബം
തിരുത്തുക- ↑ Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. volume 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122
{{citation}}:|volume=has extra text (help); Cite has empty unknown parameter:|other=(help). - ↑ Kestin, J. (1966). A Course in Thermodynamics, Blaisdell Publishing Company, Waltham MA, p. 196.
- ↑ Münster, A. (1970). Classical Thermodynamics, translated by E. S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, p. 13.
- ↑ Haase, R. (1971). Survey of Fundamental Laws, chapter 1 of Thermodynamics, pages 1–97 of volume 1, ed. W. Jost, of Physical Chemistry. An Advanced Treatise, ed. H. Eyring, D. Henderson, W. Jost, Academic Press, New York, lcn 73–117081, p. 71.
- ↑ Borgnakke, C., Sonntag., R.E. (2009). Fundamentals of Thermodynamics, seventh edition, Wiley, ISBN 978-0-470-04192-5, p. 310.
- ↑ Massey, B. S. (1970), Mechanics of Fluids, Section 12.2 (2nd edition) Van Nostrand Reinhold Company, London. Library of Congress Catalog Card Number: 67-25005, p. 19.
- ↑ Çengel, Y. A., Boles, M. A. (2015). Thermodynamics: An Engineering Approach, 8th edition, McGraw-Hill, New York, ISBN 978-0-07-339817-4, p. 340.
- ↑ Cengel, Yunus A., and Michaeul A. Boles. Thermodynamics: An Engineering Approach. 7th Edition ed. New York: Mcgraw-Hill, 2012. Print.
- ↑ Cengel, Yunus A., and Michaeul A. Boles. Thermodynamics: An Engineering Approach. 7th Edition ed. New York: Mcgraw-Hill, 2012. Print.







