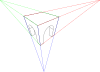
ത്രിമാന പ്രക്ഷേപം

ത്രിമാന വസ്തുക്കളെ ദ്വിമാനപ്രതലത്തിൽ പ്രദർശിപ്പിക്കാൻ ഉപയോഗിക്കുന്ന സങ്കേതമാണ‌് ത്രിമാന പ്രക്ഷേപം (3 dimensional projection or 3D Projection). വസ്തുക്കളുടെ രൂപത്തെ ആസ്പദമാക്കിയുളള ബിന്ദുചിത്രം രൂപപ്പെടുത്തുകയും ആ ബിന്ദുക്കളെ പരസ്പരം യോജിപ്പിച്ചുകൊണ്ട് ഒരു ദൃശ്യരൂപം ഉണ്ടാക്കുകയും ചെയ്യുന്നു. അങ്ങനെ കിട്ടുന്ന രൂപം യഥാർത്ഥ ത്രിമാന വസ്തുവിന്റെ ദ്വിമാനപ്രതലത്തിലുളള കാഴ്ചയായിരിക്കും നല്കുക. എൻജിനീയറിംഗ് രേഖാചിത്രങ്ങളിലും കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിലും ഇത്തരം പ്രക്ഷേപങ്ങൾ വ്യാപകമായി ഉപയോഗിച്ചുവരുന്നു. പ്രധാനമായും രണ്ടുവിധത്തിലുളള പ്രക്ഷേപരീതികളുണ്ട്:

ബഹുമുഖപ്രക്ഷേപം (Multiview projection) (മുൻകാഴ്ച,elevation)
അക്ഷമിതീയപ്രക്ഷേപം Axonometric projection അഥവാ സമനീയപ്രക്ഷേപം(isometric)
തിര്യക് പ്രക്ഷേപം (Oblique projection) (മിലിട്ടറി)
തിര്യക് പ്രക്ഷേപം (ക്യാബിനെറ്റ്)
ഏക പരിപ്രേക്ഷ്യം(One-point perspective)
ദ‌്വിക പരിപ്രേക്ഷ്യം Two-point perspective
ത്രിക പരിപ്രേക്ഷ്യം (Three-point perspective)

സമാന്തര പ്രക്ഷേപം തിരുത്തുക

അനതിവിദൂരമായ ഒരു വീക്ഷണബിന്ദുവിൽ നിന്നുളള പരിപ്രേക്ഷ്യ പ്രക്ഷേപത്തിന് സമാനമാണ് സമാന്തര പ്രക്ഷേപം

സമാന്തരപ്രക്ഷേപത്തിൽ, വസ്തുവിൽ നിന്നും പ്രക്ഷേപതലത്തിലേയ്ക്കുളള വീക്ഷണരേഖകൾ പരസ്പരം സമാന്തരമായിരിക്കും. ത്രിമാനതലത്തിലെ പരസ്പര സമാന്തരരേഖകൾ ദ്വിമാനത്തിലും അങ്ങനെ തന്നെയായിരിക്കും. അനന്തമായ കേന്ദ്രകദൂരമുള്ള (focal length) ഒരു പരിപ്രേക്ഷ്യപ്രക്ഷേപം പോലയാണ് സമാന്തരപ്രക്ഷേപം.

സമകോണീയപ്രക്ഷേപം (Orthographic projection) തിരുത്തുക

വരയ്ക്കുന്ന പ്രതലത്തിന് ലംബമായതും എന്നാൽ പരസപരം സമാന്തരമായതുമായ വീക്ഷണരേഖകളിലൂടെ ത്രിമാനവസ്തുക്കളെ വീക്ഷിക്കുന്നതായി സങ്കല്പിച്ചുകൊണ്ട് അവയെ ദ്വിമാന പ്രതലത്തിൽ പ്രതിനിധാനം ചെയ്യുന്ന രീതിയാണ‌് സമകോണീയപ്രക്ഷേപം (Orthographic projection). ഇത് സമാന്തരപ്രക്ഷപത്തിന് ഉദാഹരണമാണ്. സാധാരണയായി ഒരു ത്രിമാന വസ്തുവിനെ പ്രതിനിധാനം ചെയ്യുന്നതിന് അതിന്റെ മൂന്നു ദിശകളിലെ ഇപ്രകാരമുളള ചിത്രം ആവശ്യമാണ്.

ബഹുമുഖപ്രക്ഷേപം (Multiview projection) തിരുത്തുക

ഒരു ബഹുമുഖപ്രക്ഷേപം ഒന്നാംകോണത്തിലാണോ (വലത്) മൂന്നാം കോണത്തിലാണോ (ഇടത്) എന്നത് സൂചിപ്പിക്കുന‌്നതിനുളള പ്രതീകം

വസ്തുക്കളുടെ അക്ഷങ്ങൾക്ക് സമാന്തരമായ പ്രതലങ്ങളിൽ അവയുടെ സമാന്തരപ്രക്ഷേപങ്ങൾ നിർമ്മിക്കുന്ന രീതിയാണിത്. പ്രാഥമികമുഖങ്ങൾ (primary views) എന്നറിയപ്പെടുന്ന ആറു ചിത്രങ്ങൾ വരെ ഇപ്രകാരം നിർമ്മിക്കാൻ കഴിയും. എന്നിരുന്നാലും സാധാരണയായി ഒരു ത്രിമാനവസ്തുവിനെ പ്രതിനിധാനം ചെയ്യുന്നതിന് ഏതെങ്കിലും മൂന്നു മുഖങ്ങൾ മതിയാകും. ഇവയെ മുൻവശദൃശ്യം (front view), മുകൾദൃശ്യം (topview), പാർശ്വദൃശ്യം (endview) എന്നാണ‌് അറിയപ്പെടുക. മുൻകാഴ്ച(elevation), പ്ലാൻ, പരിച്ഛേദം(section) എന്നീ പദങ്ങളും ഉപയോഗിക്കാറുണ്ട്.

അക്ഷമീതീയ പ്രക്ഷേപം (Axonometric projection) തിരുത്തുക

മൂന്ന‌് അക്ഷമിതീയ മുഖങ്ങൾ

വസ്തുക്കളെ ചരിഞ്ഞ ദിശയിലൂടെ കാണുമ്പോഴുണ്ടാകുന്ന ബിംബമാണ് അക്ഷമിതീയ പ്രക്ഷേപം. ത്രിതലത്തിലെ എല്ലാ ദിശകളിലുമുളള കാഴ്ച ഒറ്റചിത്രത്തിൽ കാണിക്കുന്ന രീതിയാണിത്.^[1] പരിപ്രേക്ഷ്യപ്രക്ഷേപത്തിന്റെ ഏകദേശസമാനമായാണ് അക്ഷമിതീയ പ്രക്ഷേപം നിർമ്മിക്കുന്നതെങ്കിലും ഏകദേശനം (approximation) മൂലം ഇതിൽ ശ്രദ്ധേയമായ കോട്ടം ഉണ്ടാകാറുണ്ട്.^{[വ്യക്തത വരുത്തേണ്ടതുണ്ട്]}

മുഖങ്ങളുടെ സമകോണീയതയിൽ(orthogonal) നിന്നുളള കോൺവ്യതിയാനമനുസരിച്ച് അക്ഷമീതീയപ്രക്ഷേപത്തെ മൂന്നുവിഭാഗങ്ങളായി തിരിച്ചിട്ടുണ്ട്: സമനീയപ്രക്ഷേപം (isometric projection), ദ്വിമിതീയപ്രക്ഷേപം (Dimetric projection), ത്രിമിതീയപ്രക്ഷേപം (Trimetric projection) .^[2]^[3]

സമനീയ പ്രക്ഷേപം (Isometric projection) തിരുത്തുക

സമനീയപ്രക്ഷേപങ്ങളിൽ ത്രിതലത്തിലെ മൂന്നു അക്ഷങ്ങളും ഒരുപോലെ ചെറുതാക്കപ്പെടുന്നു. അവയ്ക്കിടയിലെ കോൺ 120° ആയിരിക്കും. ചെറുതാക്കപ്പെടുന്നതുമൂലം മൂന്നു അക്ഷങ്ങളിലും ഉണ്ടാകുന്ന കോട്ടം ഒരേ പോലെയായതിനാൽ നീളത്തിലും വീതിയിലും വശങ്ങളിലുമുളള ആനുപാതികത അതേപടി നിലനിർത്തപ്പെടുന്നു. ‌ചിത്രത്തിൽ നിന്നും നേരിട്ട് അളവുകൾ എടുക്കാൻ ഇതുമൂലം സാധിക്കുന്നു.

തിര്യക് പ്രക്ഷേപം (Oblique projection) തിരുത്തുക

Potting bench drawn in cabinet projection with an angle of 45° and a ratio of 2/3

Stone arch drawn in military perspective

സമകോണപ്രക്ഷേപത്തിൽ (orthographic projection) നിന്നും വ്യത്യസ്തമായി തിര്യക് പ്രക്ഷേപത്തിൽ പ്രക്ഷേപരേഖകൾ വീക്ഷണപ്രതലവുമായി 90 ഡിഗ്രിയിലല്ലാത്ത കോണിലാണ‌് പതിക്കുന്നത്. തിര്യക് പ്രക്ഷേപങ്ങൾ സരളമായതിനാൽ അവയെ കൂടുതലായും ചിത്രീകരണത്തിനായാണ് ഉപയോഗിക്കുന്നത്. വിശേഷപ്പെട്ട തിര്യക് പ്രക്ഷേപങ്ങൾ താഴെപ്പറയുന്നു:

കവലിയർ പ്രക്ഷേപം (45°) തിരുത്തുക

വസ്തുവിലെ ഒരു ബിന്ദുവിനെ x, y, z എന്നീ മൂന്നു അങ്കങ്ങളുപയോഗിച്ച് പ്രതിനിധീകരിക്കുകയും വരയ്ക്കുമ്പോൾ x″ , y″ എന്നീ രണ്ടു അങ്കങ്ങൾ മാത്രം ഉപയോഗിക്കുകയും ചെയ്യുന്നു. x, z അക്ഷങ്ങൾ പരസ്പരം ലംബമാണെങ്കിൽ y അക്ഷം x″ ന് 30° യോ 45° യോ ആയിരിക്കും. മൂന്നാം അക്ഷത്തിന്റെ നീളം തോതനുസരിച്ചായിരിക്കില്ല.

ക്യാബിനെറ്റ് പ്രക്ഷേപം തിരുത്തുക

വീക്ഷണവസ്തുവിന്റെ ഒരു മുഖം വീക്ഷണതലത്തിന് സമാന്തരമായതും മൂന്നാം അക്ഷം 30° യോ 45° യോ ചരിവിലുമായിരിക്കും. എന്നാൽ കവലിയറിൽ നിന്നും വ്യത്യസ്തമായി ഇതിൽ മൂന്നാം അക്ഷത്തിന്റെ നീളം പകുതിമാത്രമേ ഉണ്ടാകുകയുളളു.

മിലിട്ടറി പ്രക്ഷേപം തിരുത്തുക

തിര്യക് പ്രക്ഷേപത്തിന്റെ ഒരു വകഭേദമാണ് മിലിട്ടറി പ‌്രക്ഷേപം. ഇതിൽ പ്ലാനുകൾക്ക് കോട്ടം വരാത്തവിധം തിരശ്ചീന തലങ്ങൾ സമലംബാക്ഷീയമായി (isometrically) വരയ്ക്കുന്നു. പക്ഷേ ലംബരേഖകൾ ചരിച്ചാണ് വരയ്ക്കുക. xy തലത്തിലുളള കറക്കവും z തലത്തിലുളള ലംബ വിസ്ഥാപനവും (vertical translation) ആണ് മിലിട്ടറി പ്രക്ഷേപം. ^[4]

↑ Mitchell, William; Malcolm McCullough (1994). Digital design media. John Wiley and Sons. p. 169. ISBN 978-0-471-28666-0.
↑ Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. p. 22. ISBN 978-0-8014-7280-0.
↑ McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. p. 502. ISBN 978-1-55860-659-3.
↑ "Axonometric projections - a technical overview". Retrieved 24 April 2015.

[1] Mitchell, William; Malcolm McCullough (1994). Digital design media. John Wiley and Sons. p. 169. ISBN 978-0-471-28666-0.

[maynard-2] Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. p. 22. ISBN 978-0-8014-7280-0.

[mcreynolds-3] McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. p. 502. ISBN 978-1-55860-659-3.

[4] "Axonometric projections - a technical overview". Retrieved 24 April 2015.

[1]

[2]

[3]

[4]